正常电梯可以并行站立 2 个人通行,但在上班高峰时,电梯就被分成了 2 侧,一侧用于那些想要快速走过的人,一侧用于那些正常乘坐电梯的人。
每次上下班通过电梯时看到拥堵的人群,总是忍不住去想,这种分成 2 侧的方案对于整体来说到底是快了还是慢了?第一感觉是不是觉得肯定有加速通道的快?
我打算自己估算一下。
01
—
前提准备
**方案划分:**我把这两种方案起一个名字,方便后续说明,就叫:
方案 1: 并行 2 人站立通过的方式
方案 2:有加速通道的方式
电梯速度:我自行通过站立和行走的方式,测量了 2 种方式通过电梯的时长,站立的时长大约为行走时的 2 倍,所以为了方便计算,我就这样定义速度:
方案 1:站立通过速度为 1/s,也就是并行情况下,1s 可以通行 2 人
方案 2:行走通过速度为 2/s,也就是并行情况下,1s 可以通行 4 人
人员行走比率:我通过观察统计大致估算了一下比率为 30% 左右,这只是用来对比,不用很准。
02
—
人数固定,哪种耗时最短?
方案 1:人数 / 2 就是所需时间。
方案 2:根据人员比率计算出总速度,然后求出总时间。
得出结果:
并行耗时 比率:1.00,速度:1.0,耗时:50.0
加速耗时 比率:0.30,速度:4.5,耗时:48.8
加速耗时 比率:0.40,速度:4.0,耗时:45.5
加速耗时 比率:0.50,速度:3.5,耗时:44.4
加速耗时 比率:0.90,速度:3.0,耗时:35.7
根据这个结果发现:
方案 2:在加速比率为 30% 参与时,速度要站立的 4.5 倍才可以更优;数据有点奇怪
思考了一下后,发现这个思路有问题:
-
假设了所有加速的人和不加速的人,分开 2 侧,都已经排好了队
-
以最后一人通过的节点来判断了通过时间;也就是最后一个不加速的人通过的时间 这不符合常理;
所以我想那计算不同策略下的运载量是不是可行
03
—
时间固定,哪种运载量更大?
方案 1:2 * 时长 就是所求的运载量。
方案 2:根据人员比率计算出总速度,然后乘以时间,求出运载量。
结果如下:
并行耗时 比率:1.00,速度:1.0,运载量:60.0
加速耗时 比率:0.10,速度:2.0,运载量:66.0
加速耗时 比率:0.20,速度:2.0,运载量:72.0
加速耗时 比率:0.30,速度:2.0,运载量:78.0
加速耗时 比率:0.40,速度:2.0,运载量:84.0
根据这个结果发现:
策略 2,只要 10% 人参与行走,就能比 策略 1 的运载量大,这感觉也不对,不符合实际
我想关键问题还是这个:
- 我假设了所有加速的人和不加速的人,分开 2 侧,都已经排好了队
这个不符合现实,这样算出来的运载量只是最好的情况;
正常情况下的人群是混着快速行走和不快速行走的人,而且如果不行走的人比例高的话,还会挡着另一侧的快速通道,导致想行走的人也上不去只能排队;
我试着模拟一下真实情况
04
—
人员随机分布,时间固定,哪种运载量更大?
方案 1:2 * 时长 就是所求的运载量。和上次一样
方案 2:
-
加速人员根据比例随机分布
-
思考出 7 种上电梯模型,根据模型计算,对应时长下的运载量,大致模型如图:
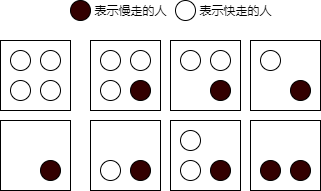
-
计算不同比率加速人群下的运载量
结果如图:
根据这个结果发现:
方案 2,在 56% 的行走人员时,运载量会基本和 方案 1 持平; 但如果小于 56% 的人选择行走,则不如方案 1 好。
05
—
总结
个人与整体,从个人角度来看,肯定是可以快走的方案更好,这节省了个人时间;但从整体看,却有可能是拖累。
这也好理解,这相当于牺牲了大多数人另一侧通道站立的机会,给少数要快速行走的人让出了一个通道。
可能不完全准确,但却值得深思
代码地址:https://github.com/hui1hui2hui3/dttd